Notes on Intersil AN9757

Tessellated Circuits: Home Old Home OA designer SS OA notes  

Introduction

The two single supply modes of this calculator are based on Intersil's Application Note number AN9757 (the version dated September, 2002 was the latest at the time of this writing, and it has not been revised even by early 2013). A similar treatment appears in TI's “Op Amps For Everyone”, document SLD0006B, by Ron Mancini (this is such a comprehensive document that it became a book and it has a price tag now, however, an earlier revision B (464 pp!) is available on-line, see here, on TI's site).

Intersil AN9757 Errata:

These are a few things that I noticed, the first two are semi-critical:

• EQ. 8 should read y = +mx -b ^*1;
• EQ. 10 should read y = -mx +b ^*1;
• In Design Example #1, R4/R3 is closer to 3.06 than 3 ^*2;
• In Design Example #2, R2/R1 actually calculates as 49, not 50 ^*2;
• In Design Example #3, R6/R5 actually calculates as 394, not 390 ^*2.

^*1Why is it always the simplest equations that get messed up?

^*2OK, if you think I'm being silly, then perhaps you can explain why the App Note's authors used 66.66 in Example #1 and 7.777 in Example #3? Seriously, it is always good to keep the precision of your calculations consistent with the accuracy of the components being used. The values selected in the App Note seem to be all 5% tolerance parts, so none of these differences noted would be significant, but they could be if 1% components were selected.

A Clarification:

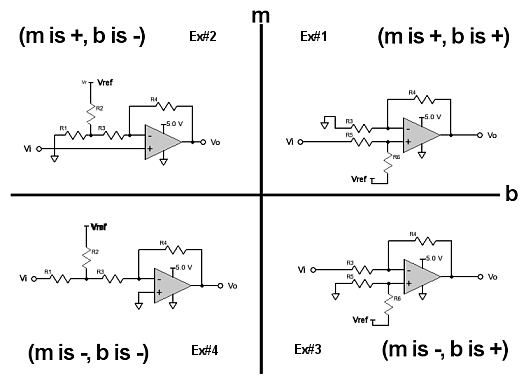
One of my reviewers has pointed out that the way that algebraic notation is abused can be confusing. The problem is in the straight line equation y=mx+b. Implying that there are four separate versions (+mx+b, +mx-b, -mx+b and -mx-b) is the problem. What the authors of the Intersil app note (the TI one is not guilty of this form of algebraic abuse) mean is that the solutions, in terms of the circuit configurations, fall into 4 categories and that these categories are determined by the signs of m and b. The figure below should make this clear. (The numbers for each of the App Note's 4 worked examples are shown for reference.)

Get real!

There are several classes of degenerate cases.

• If m is zero, no gain is required so this is the same as an open circuit, or, if there is an offset (y=b) then the offset becomes the output. When this condition is encountered, a notice is given and really high, fake values are given to all resistors.
• When both m and b are positive but m (the slope: the gain) is less than 1 is another special case. It is well known that the gain of a non inverting op amp is {1+ a resistor ratio}, so this cannot be implemented without attenuating the input voltage sufficiently for the gain to be above 1. I added a warning to the text but did not try to suggest an attenuator design. (Note: the Thevenin resistance of any attenuator will affect the value of R5.)
• Similarly, when m is positive and b is negative, but m is less than 1 also requires attenuation on the positive input. If this is the case Design Example #2's assumption that R6 is open and R5 is shorted can be over-ridden and these can be used as an attenuator to make the required gain >1. I have handled this by configuring the R5/(R5+R6) attenuator, and forcing the Op Amp into follower mode by making R4=0.

A Dose of Practicality:

I generalized the calculations to use a reference voltage instead of the positive supply. Often, in a real system one would take the step of generating a reference voltage that is half the supply voltage and be done with it. This means that—assuming the incoming signals are referenced to this voltage—the dual supply techniques, circuit configurations and calculations can be adopted. This is something that the Intersil App note does not really admit. On the other hand, since these techniques are very generalized, they can be used in systems where the reference voltage is at some level other than what incoming signals are referenced to, and/or where the supply voltage is sufficiently accurate to allow it to be used as a reference.

So, rather than using the confusing “V_cc+” and “V_cc-” I use “V_b2” and “V_b1” respectively, instead. Once the limiting associations with the power supply voltage are removed it becomes obvious that these two voltages can be any (reasonable) value. As mentioned, often another bias voltage is used. This can be either a reference voltage or a buffered version of half the supply.

Implementation notes:

In each case, below, the highlighted design examples are links to the calculator with the values already filled in, one for each of the App Note's examples.

In Design Example #1 , I think that it is better to think in terms of Vb1 being 0 V, not to say that it is not needed. This makes R2=0 and R1=open, which is opposite what the app note says. Algebraically it does not matter, mostly this is a matter of convenience for the drawing since it is simpler to not have to draw an input grounded. In fact, if you examine the equations for each case, the terms of EQ. 13 (used by Example 4) are the ones not present in EQ. 7 (the present example). Both of these terms are being forced to 0. Several combinations of making R2=0 or R1=0 or V_i-=0 or V_b1=0 do the trick, as long as each term has a zero factor multiplied.

Similarly, in Design Example #4 , I think in terms of Vb2 being 0 V, and not to say that it is not needed. This makes R6=0 and R5=open, opposite to what the App Note says.

In Design Example #2 , the App Note makes the simplification, to get from EQ. 16 to EQ. 18, that R6/(R6+R5) = 1. Algebraically, I'm pretty sure that ∞/(0+∞) is more like 1 than 0/(∞+0), which would become 0/((1/0)+0), and appears to be 0. So making R6=∞ is appropriate.

While looking into Design Example #2, it should be noted that a simplification can be made: if the Vb1, R2, R1 network is replaced by a reference voltage equal to Vb1(R1/(R1+R2) (and no connection to ground is made), we get a pretty standard configuration where the negative terminal is referenced to a different voltage than the supply.

Yet another comment about this example is that the choice of R1 and R2 should be such that their Thevinin equivalent resistance should be low enough that it does not affect the outcome significantly. This is not stated in the app note. How low it should be would likely be best determined by the tolerance of the resistors used: R2||R1 would be best if they were less than R3 by, say, half of R3's tolerance. This is not implemented, but see the next paragraph. How low these can go depends on the capacity and accuracy under load of the reference voltage, and the system power consumption goals—all things that this software doesn't ask of the designer.

When I built up versions of all 4 of these circuits I found that this one did not produce accurate results. I had tried a variation whereby I was using a 1.25 V reference instead of the supply and the Thevenin equivalent resistance increased so much that the assumption made to simplify the equations did not hold. I've modified the analysis software to look for this condition and re-calculate the outputs with the reality in mind: the suggesting software, however, does not take the Thevenin equivalent into account. To work around a situation where the output is too far off the desired values, increase R3 and R4 and/or decrease R1 and R2, but keep the R2/R1 and R4/R3 ratios both the same. These kind of changes can be made easily in the analysis mode.

Design Example #3  has a simplification, where R2/(R1+R2) becomes 1 by assuming that R2=∞ and R1=0. Note that the values chosen for R3 and R4 are set by the limit on the maximum resistor rather than picking that commom value of 10 kΩ for one of them as was (probably) done by the app note authors.